xpycc's Blog

都说 Splay 不仅仅是平衡树那么简单，由于它可以任意旋转，它还可以高效完成一些在区间上的操作，于是就做了几道 Splay 的题目。虽然不是很难，但很巧妙，也确实很烦，所以就取了 "Boring Sequence Manipulation" 这个标题，呵呵~ 下面进入正题。

其实 Splay 高效做区间操作的原理和线段树几乎一样，都是标记延迟，都是从根到叶，在维护的时候，也都是从叶到根的维护。只是 Splay 可以改变根和叶的关系，而线段树的根叶关系则不能改变。因而Splay 可以实现任意插入和删除结点，更为轻松地实现旋转(rotate)、翻转(reverse) 等操作。然而，这不是没有代价的，因为每次做 splay/rotate 操作时都会要求立即还原被延迟的标记，使被旋转结点能够正确地被维护，所以这样会有更大的常数。而且 Splay 的码量也较线段树大。

然而实际做题的时候，问题最大的还是标记延迟的实现，这也是写线段树的关键点。鉴于以往线段树的实践，与线段树一样，我的做法是，父结点的标记都是给儿子结点做的。也就是说，父结点的标记表示的确切意义是，父结点的信息已维护，子结点的信息未维护。这就很好地对应了 rotate 的意图，push_down 为的就是使子结点的信息得到更正，而不是父结点自己的信息得到更正。相应地，从 splay/rotate 的实现中可以看出，update 总是假定父结点的标记已传给子结点，即假定 update 之前一定做过 push_down 。于是两者结合，就可以保证正确性了。

更详细地，所有结点的信息有三类，标记信息、固有信息、子结点相关信息。其中，第一个和第三个是和线段树一致的，第三个由于经常和要求的答案有直接关系，所以也被称为答案信息。由于 splay 的结点，其本身是序列中的一个元素，所以，较线段树来说，又多了一个固有信息，即与子结点无关的信息。push_down 的作用就是维护子结点固有信息和答案信息，而 update 的作用就是根据固有信息和  新建立父子关系的子结点  的信息，维护其本身的答案信息。由于 splay 的结点，同一般的树一样，既可以看成是一个结点，也可以看成是一棵子树。因而，在从某个结点到树根路径的旋转过程中，可以到最后才 update 。因为在这条路径中，从父结点 push_down 保证了固有信息的正确性，虽然在 push_down 的过程中，答案信息是错误的，但是终将会在最后的 update 操作中得到更正。并且，对该结点的 push_down ，起到了一个传递信息的作用，保证了旋转过程中 其临时子结点 的信息的正确性，这点保证了路径上其他结点的 update 操作是正确的。又由于该结点的答案信息只与固有信息和 最后建立父子关系 的子结点的答案信息有关，所以可以省去中间过程中的 update 操作。再结合 push_down 保证了固有信息的正确性，而且 update 在 push_down 之后，满足 update 的假设，所以这样做是正确的，固有信息和答案信息的正确性都得到了保证。

最后就是 mark_xxx 函数，其作用是对于给定标记，维护某个结点的固有信息和答案信息，并做上标记。事实上 push_down 也是用它来实现的，在标记信息有多个的时候 push_down 实现对子结点做何种标记，即调用哪个 mark_xxx 函数。

另外，每次做完标记，或者单独更新（对于那些只更新单个结点的题目来说）的时候，最好把其父结点转到根的位置，保证整棵树的正确性（对于那些只更新单个结点的题目，还可以提高效率）。事实上，平常的带 _size 域实现的 Splay 平衡树的删除结点操作就是这样来完成的。

那么，了解原理之后，对于这些函数做出设定，其他的基本上就可以交给模板来完成了。

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define MAXMEM 100010

template <class T>
struct Splay {
	struct Node {
		Node *_fa, *_ch[2];
		T _val;
		Node *_min_node;
		int _size;
		bool _rev;

		Node* get_end(int c) {			// 0 表示左端 1 表示右端
			Node* x = this;
			while (x->_ch[c]) {
				x->push_down();			// notice!
				x = x->_ch[c];
			}
			return x;
		}

		Node* get_near(int c) {
			if (_ch[c])
				return _ch[c]->get_end(1 - c);
			Node* x = this;
			while (x->_fa && x->_fa->_ch[c] == x)
				x = x->_fa;
			return x->_fa;
		}

		Node* get_succ() { return get_near(1); }
		Node* get_prev() { return get_near(0); }

		int get_size() {		// 兼容 this == 0
			if (this) return _size;
			else return 0;
		}

		void mark_node() {
			if (this) {
				_rev = !_rev;
				swap(_ch[0], _ch[1]);
			}
		}

		void push_down() {				// 向下传标记
			if (_rev) {
				_ch[0]->mark_node();
				_ch[1]->mark_node();
				_rev = false;
			}
		}

		void update() {					// 向上更新，可以为空
			_size = 1 + _ch[0]->get_size() + _ch[1]->get_size();
			_min_node = this;
			if (_ch[0] && _ch[0]->_min_node->_val < _min_node->_val)
				_min_node = _ch[0]->_min_node;
			if (_ch[1] && _ch[1]->_min_node->_val < _min_node->_val)
				_min_node = _ch[1]->_min_node;
		}
	};

	Node *_root;
	static Node *const _fa_root, _nodes[MAXMEM];

	void rotate(Node* x, int c) {    // 旋转操作，0 表示左旋，1 表示右旋
		Node* y = x->_fa;
		y->push_down(); x->push_down(); // y 在 x 之上，故先 y 后 x
		y->_ch[1 - c] = x->_ch[c];
		if (x->_ch[c])
			x->_ch[c]->_fa = y;
		x->_fa = y->_fa;
		if (y->_fa != _fa_root) {
			if (y->_fa->_ch[0] == y)
				y->_fa->_ch[0] = x;
			else
				y->_fa->_ch[1] = x;
		} else
			_root = x;
		x->_ch[c] = y;
		y->_fa = x;
		y->update();						// 维护 y
	}

	void splay(Node* x, Node *f) {    // 把结点 x 转到结点 f 下面
		x->push_down();
		while (x->_fa != f) {
			if (x->_fa->_fa == f) {
				if (x->_fa->_ch[0] == x)
					rotate(x, 1);
				else
					rotate(x, 0);
			} else {
				Node *y = x->_fa, *z = y->_fa;
				if (z->_ch[0] == y) {
					if (y->_ch[0] == x)
						rotate(y, 1), rotate(x, 1);
					else
						rotate(x, 0), rotate(x, 1);
				} else {
					if (y->_ch[1] == x)
						rotate(y, 0), rotate(x, 0);
					else
						rotate(x, 1), rotate(x, 0);
				}
			}
		}
		x->update();
	}

	void build(int a, int b) {
		_root = make_tree(a, b);
		_root->_fa = _fa_root;
	}

	static Node* make_tree(int a, int b) {
		if (a > b)
			return 0;
		Node* root = _nodes + (a + b) / 2;
		root->_rev = false;
		root->_ch[0] = make_tree(a, root - _nodes - 1);
		if (root->_ch[0])
			root->_ch[0]->_fa = root;
		root->_ch[1] = make_tree(root - _nodes + 1, b);
		if (root->_ch[1])
			root->_ch[1]->_fa = root;
		root->update();
		return root;
	}
};

template <class T>
typename Splay<T>::Node *const Splay<T>::_fa_root = 0;
	
template <class T>
typename Splay<T>::Node Splay<T>::_nodes[MAXMEM];

Splay<pair<int, int> > tree;

int main() {
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
	int n;
	while (scanf("%d", &n) != EOF) {
		if (n == 0)
			break;
		for (int i = 1; i <= n; ++i) {
			scanf("%d", &tree._nodes[i]._val.first);
			tree._nodes[i]._val.second = i;
		}
		tree._nodes[n + 1]._val = make_pair(0x7fffffff, 0x7fffffff);
		tree.build(0, n + 1);
		Splay<pair<int, int> >::Node * min_node = tree._nodes, *min_succ;
		for (int i = 1; i < n; ++i) {
			tree.splay(min_node, tree._fa_root);
			min_node = tree._root->_ch[1]->_min_node;
			tree.splay(min_node, tree._root);
			min_succ = min_node->get_succ();
			tree.splay(min_succ, tree._root);
			printf("%d ", i - 1 + min_succ->_ch[0]->get_size());
			min_succ->_ch[0]->mark_node();
		}
		printf("%d\n", n);
	}
    return 0;
}

简单的不带删除的翻转，push_down 、mark_node(以后叫 mark_rev) 和 update 写完了以后，就可以把任务交给模板了，不过要注意，由于翻转，所以 get_succ 的时候，要在路径上做维护，也就是不断地 push_down ，来得到真正的后继。不过其实这是在 get_end 里面完成的，因为已经旋转到根的下面，而且根已经被更新，所以可以直接调 get_succ ，因为它一定会调用 get_end 。所以更加严谨一些的话应该写 get_end ，不过由于意义上 get_succ 更明了，所以就写 get_succ 了。而且，对于有 _rev 这种信息的树来说，get_end 就必须要通过 push_down 来保证正确性。

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define MAXN 100000

const int MAXMEM = MAXN * 3 + 2;

int ans[MAXMEM], tot;

template <class T>
struct Splay {
	struct Node {
		Node *_fa, *_ch[2];
		T _val;
		int _size;
		bool _rev;

		Node* get_end(int c) {			// 0 表示左端 1 表示右端
			Node* x = this;
			x->push_down();				// notice!
			while (x->_ch[c]) {
				x = x->_ch[c];
				x->push_down();			// notice!
			}
			return x;
		}

		Node* get_near(int c) {
			if (_ch[c])
				return _ch[c]->get_end(1 - c);
			Node* x = this;
			while (x->_fa && x->_fa->_ch[c] == x)
				x = x->_fa;
			return x->_fa;
		}

		Node* get_succ() { return get_near(1); }
		Node* get_prev() { return get_near(0); }

		int get_size() {		// 兼容 this == 0
			if (this) return _size;
			else return 0;
		}

		void mark_node() {
			if (this) {
				_rev = !_rev;
				swap(_ch[0], _ch[1]);
			}
		}

		void push_down() {				// 向下传标记
			if (_rev) {
				_ch[0]->mark_node();
				_ch[1]->mark_node();
				_rev = false;
			}
		}

		void update() {					// 向上更新，可以为空
			_size = 1 + _ch[0]->get_size() + _ch[1]->get_size();
		}

		void travel() {
			push_down();
			if (_ch[0]) _ch[0]->travel();
			ans[tot++] = _val;
			if (_ch[1]) _ch[1]->travel();
		}
	};

	Node *_root;
	static Node *const _fa_root, _nodes[MAXMEM];

	void rotate(Node* x, int c) {    // 旋转操作，0 表示左旋，1 表示右旋
		Node* y = x->_fa;
		y->push_down(); x->push_down(); // y 在 x 之上，故先 y 后 x
		y->_ch[1 - c] = x->_ch[c];
		if (x->_ch[c])
			x->_ch[c]->_fa = y;
		x->_fa = y->_fa;
		if (y->_fa != _fa_root) {
			if (y->_fa->_ch[0] == y)
				y->_fa->_ch[0] = x;
			else
				y->_fa->_ch[1] = x;
		} else
			_root = x;
		x->_ch[c] = y;
		y->_fa = x;
		y->update();						// 维护 y
	}

	void splay(Node* x, Node *f) {    // 把结点 x 转到结点 f 下面
		x->push_down();
		while (x->_fa != f) {
			if (x->_fa->_fa == f) {
				if (x->_fa->_ch[0] == x)
					rotate(x, 1);
				else
					rotate(x, 0);
			} else {
				Node *y = x->_fa, *z = y->_fa;
				if (z->_ch[0] == y) {
					if (y->_ch[0] == x)
						rotate(y, 1), rotate(x, 1);
					else
						rotate(x, 0), rotate(x, 1);
				} else {
					if (y->_ch[1] == x)
						rotate(y, 0), rotate(x, 0);
					else
						rotate(x, 1), rotate(x, 0);
				}
			}
		}
		x->update();
	}

	Node* find_kth(int k) {
		Node* x = _root;
		x->push_down();				// notice!
		while (k != x->_ch[0]->get_size() + 1) {
			if (k <= x->_ch[0]->get_size()) {
				x = x->_ch[0];
			} else {
				k -= x->_ch[0]->get_size() + 1;
				x = x->_ch[1];
			}
			x->push_down();			// notice!
		}
		return x;
	}

	void build(int a, int b) {
		_root = make_tree(a, b);
		_root->_fa = _fa_root;
	}

	static Node* make_tree(int a, int b) {
		if (a > b)
			return 0;
		Node* root = _nodes + (a + b) / 2;
		root->_rev = false;
		root->_ch[0] = make_tree(a, root - _nodes - 1);
		if (root->_ch[0])
			root->_ch[0]->_fa = root;
		root->_ch[1] = make_tree(root - _nodes + 1, b);
		if (root->_ch[1])
			root->_ch[1]->_fa = root;
		root->update();				// notice!
		return root;
	}

	void dispaly() {
		tot = 0;
		_root->travel();
	}
};

template <class T>
typename Splay<T>::Node *const Splay<T>::_fa_root = 0;
	
template <class T>
typename Splay<T>::Node Splay<T>::_nodes[MAXMEM];

Splay<int> tree;
char buf[100];

int main() {
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
	int n, m;
	while (scanf("%d%d", &n, &m) != EOF) {
		if (n < 0 && m < 0)
			break;
		for (int i = 1; i <= n + 1; ++i)
			tree._nodes[i]._val = i;
		tree.build(0, n + 1);
		for (int i = 0; i < m; ++i) {
			scanf("%s", buf);
			int a, b, c;
			if (buf[0] == 'C') {
				scanf("%d%d%d", &a, &b, &c);
				tree.splay(tree.find_kth(a), tree._fa_root);
				tree.splay(tree.find_kth(b + 2), tree._root);
				Splay<int>::Node* handle = tree._root->_ch[1]->_ch[0];
				tree._root->_ch[1]->_ch[0] = 0;
				tree.splay(tree._root->_ch[1], tree._fa_root);

				tree.splay(tree.find_kth(c + 1), tree._fa_root);
				tree.splay(tree._root->get_succ(), tree._root);
				tree._root->_ch[1]->_ch[0] = handle;
				handle->_fa = tree._root->_ch[1];		// notice;
				tree.splay(tree._root->_ch[1], tree._fa_root);
			} else {
				scanf("%d%d", &a, &b);
				tree.splay(tree.find_kth(a), tree._fa_root);
				tree.splay(tree.find_kth(b + 2), tree._root);
				tree._root->_ch[1]->_ch[0]->mark_node();
				tree.splay(tree._root->_ch[1], tree._fa_root);
			}
		}
		tree.dispaly();
		for (int i = 1; i <= n; ++i) {
			if (i != 1) putchar(' ');
			printf("%d", ans[i]);
		}
		putchar('\n');
	}
    return 0;
}

带删除和插入以及查询第 k 个结点的区间翻转，基本同上，find_kth 跟 get_end 一样，在 _rev 环境下需要 push_down 保证正确性。本机调试的时候忘记维护父指针了，结果爆栈。

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define MAXN 100000

const int MAXMEM = MAXN * 2 + 1;

int pick[MAXN + 1], tot;
pair<int, int> seg[MAXN * 2 + 1];
int stot;

template <class T>
struct Splay {
	struct Node {
		Node *_fa, *_ch[2];
		T _val;
		int _size;

		Node* get_end(int c) {			// 0 表示左端 1 表示右端
			Node* x = this;
			x->push_down();				// notice!
			while (x->_ch[c]) {
				x = x->_ch[c];
				x->push_down();			// notice!
			}
			return x;
		}

		Node* get_near(int c) {
			if (_ch[c])
				return _ch[c]->get_end(1 - c);
			Node* x = this;
			while (x->_fa && x->_fa->_ch[c] == x)
				x = x->_fa;
			return x->_fa;
		}

		Node* get_succ() { return get_near(1); }
		Node* get_prev() { return get_near(0); }

		int get_size() {		// 兼容 this == 0
			if (this) return _size;
			else return 0;
		}

		void push_down() {}				// 向下传标记

		void update() {					// 向上更新，可以为空
			_size = _val.second - _val.first + 1
				+ _ch[0]->get_size() + _ch[1]->get_size();
		}
	};

	Node *_root;
	static Node *const _fa_root, _nodes[MAXMEM];

	void rotate(Node* x, int c) {    // 旋转操作，0 表示左旋，1 表示右旋
		Node* y = x->_fa;
		y->push_down(); x->push_down(); // y 在 x 之上，故先 y 后 x
		y->_ch[1 - c] = x->_ch[c];
		if (x->_ch[c])
			x->_ch[c]->_fa = y;
		x->_fa = y->_fa;
		if (y->_fa != _fa_root) {
			if (y->_fa->_ch[0] == y)
				y->_fa->_ch[0] = x;
			else
				y->_fa->_ch[1] = x;
		} else
			_root = x;
		x->_ch[c] = y;
		y->_fa = x;
		y->update();						// 维护 y
	}

	void splay(Node* x, Node *f) {    // 把结点 x 转到结点 f 下面
		x->push_down();
		while (x->_fa != f) {
			if (x->_fa->_fa == f) {
				if (x->_fa->_ch[0] == x)
					rotate(x, 1);
				else
					rotate(x, 0);
			} else {
				Node *y = x->_fa, *z = y->_fa;
				if (z->_ch[0] == y) {
					if (y->_ch[0] == x)
						rotate(y, 1), rotate(x, 1);
					else
						rotate(x, 0), rotate(x, 1);
				} else {
					if (y->_ch[1] == x)
						rotate(y, 0), rotate(x, 0);
					else
						rotate(x, 1), rotate(x, 0);
				}
			}
		}
		x->update();
	}

	Node* join(Node* r1, Node* r2) {
		if (r1 && r2) {
			Node *right_end = r1->get_end(1);
			splay(right_end, r1->_fa);
			right_end->_ch[1] = r2;
			r2->_fa = right_end;
			right_end->update();		// notice!
			return right_end;
		}
		if (r1) return r1;
		if (r2) return r2;
		return 0;
	}

	int find_kth_number(int k) {
		Node* x = _root;
		x->push_down();				// notice!
		while (
			!(x->_ch[0]->get_size() < k &&
			k <= x->_ch[0]->get_size() + x->_val.second - x->_val.first + 1)
		) {
			if (k <= x->_ch[0]->get_size()) {
				x = x->_ch[0];
			} else {
				k -= x->_ch[0]->get_size() + x->_val.second - x->_val.first + 1;
				x = x->_ch[1];
			}
			x->push_down();			// notice!
		}
		int res = x->_val.first - 1 + k - x->_ch[0]->get_size();
		splay(x, _fa_root);
		return res;
	}
	
	void delete_node(Node* nd) {
		Node* x = join(nd->_ch[0], nd->_ch[1]);
		if (nd->_fa == _fa_root) {
			_root = x;
		} else {
			if (nd->_fa->_ch[0] == nd)
				nd->_fa->_ch[0] = x;
			else
				nd->_fa->_ch[1] = x;
		}
		if (x)
			x->_fa = nd->_fa;
		if (nd->_fa)
			splay(nd->_fa, _fa_root);
	}

	void build(int a, int b) {
		_root = make_tree(a, b);
		_root->_fa = _fa_root;
	}

	static Node* make_tree(int a, int b) {
		if (a > b)
			return 0;
		Node* root = _nodes + (a + b) / 2;
		root->_val = seg[(a + b) / 2];
		root->_ch[0] = make_tree(a, root - _nodes - 1);
		if (root->_ch[0])
			root->_ch[0]->_fa = root;
		root->_ch[1] = make_tree(root - _nodes + 1, b);
		if (root->_ch[1])
			root->_ch[1]->_fa = root;
		root->update();				// notice!
		return root;
	}
};

template <class T>
typename Splay<T>::Node *const Splay<T>::_fa_root = 0;
	
template <class T>
typename Splay<T>::Node Splay<T>::_nodes[MAXMEM];

Splay<pair<int, int> > tree;
char buf[100];

int n, m;

struct Query {
	char _c;
	int _x;
} q[MAXN];

int main() {
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
	int test;
	scanf("%d", &test);
	for (int cas = 1; cas <= test; ++cas) {
		scanf("%d%d", &n, &m);

		tot = 0;
		for (int i = 0; i < m; ++i) {
			scanf("%s%d", buf, &q[i]._x);
			q[i]._c = buf[0];
			if (q[i]._c != 'R')
				pick[tot++] = q[i]._x;
		}

		sort(pick, pick + tot);
		tot = unique(pick, pick + tot) - pick;
		pick[tot] = n + 1;
		stot = 0;
		if (pick[0] != 1)
			seg[stot++] = make_pair(1, pick[0] - 1);
		for (int i = 0; i < tot; ++i) {
			seg[stot++] = make_pair(pick[i], pick[i]);
			if (pick[i] + 1 != pick[i + 1])
				seg[stot++] = make_pair(pick[i] + 1, pick[i + 1] - 1);
		}

		tree.build(0, stot - 1);
		printf("Case %d:\n", cas);
		for (int i = 0; i < m; ++i) {
			if (q[i]._c == 'T') {
				int pos = lower_bound(seg, seg + stot, make_pair(q[i]._x, q[i]._x)) - seg;
				Splay<pair<int, int> >::Node* nd = tree._nodes + pos;
				tree.delete_node(nd);
				nd->_fa = tree._fa_root;
				nd->_ch[0] = 0;	nd->_ch[1] = tree._root;
				if (tree._root)				// notice!
					tree._root->_fa = nd;
				tree._root = nd; nd->update();
			} else if (q[i]._c == 'Q') {
				int pos = lower_bound(seg, seg + stot, make_pair(q[i]._x, q[i]._x)) - seg;
				Splay<pair<int, int> >::Node* nd = tree._nodes + pos;
				tree.splay(nd, tree._fa_root);
				printf("%d\n", tree._root->_ch[0]->get_size() + 1);
			} else {	// 'R'
				printf("%d\n", tree.find_kth_number(q[i]._x));
			}
		}
	}
    return 0;
}

这题没有 push_down ，应该说更简单些吧。Splay 上的离线化操作，由于 Top 的特殊性，所以可以离散化后，根据内存的固定性，离线来做。如果 Top x 是说当前第 x 个人到前端，那么可以用动态新建结点，动态插入来实现。这题我刚开始忘记考虑删除之后，可能会得到空树了，结果 RE =          =... 之前都是 1Y 的，没想到在这题上被打破了。

#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
#define MAXMEM 500002

int arr[MAXMEM];

template <class T>
struct Splay {
	struct Node {
		Node *_fa, *_ch[2];
		T _val, _clear_val, _sum, _max_rsum, _max_lsum, _max_sum;
		int _size;		// _size 可以不要，标记这里加
		bool _rev, _clr;

		int get_size() {		// 兼容 this == 0
			if (this) return _size;
			else return 0;
		}

		int get_sum() {
			if (this) return _sum;
			else return 0;
		}

		int get_max_lsum() {
			if (this) return _max_lsum;
			else return 0;
		}

		int get_max_rsum() {
			if (this) return _max_rsum;
			else return 0;
		}

		Node() {}
		Node(const T& x) { set_value(x); }

		void *operator new(size_t) {
			if (_stop != 0) return _st[--_stop];
			else return _nodes + _mtot++;
		}

		void operator delete(void* p, size_t) {
			_st[_stop++] = (Node*)p;
		}

		void recycle() {
			if (_ch[0]) _ch[0]->recycle();
			if (_ch[1]) _ch[1]->recycle();
			delete this;
		}

		void set_value(const T& x) {
			_val = x; _size = 1;
			_rev = _clr = false;
			_sum = _max_sum = x;
			_max_lsum = max(0, x);
			_max_rsum = max(0, x);
			_ch[0] = _ch[1] = 0;
			_fa = _fa_root;
		}

		void mark_rev() {
			if (this && !_clr) {
				_rev = !_rev;
				swap(_ch[0], _ch[1]);
				swap(_max_lsum, _max_rsum);
			}
		}

		void mark_clear(const T& v) {
			if (this) {
				_clr = true;
				_clear_val = _val = v;			// notice!
				_sum = v * _size;
				_max_lsum = max(0, v * _size);
				_max_rsum = max(0, v * _size);
				_max_sum = max(v, v * _size);
				_rev = false;
			}
		}

		void push_down() {				// 向下传标记
			if (_rev) {
				_ch[0]->mark_rev();
				_ch[1]->mark_rev();
				_rev = false;
			} else if(_clr) {
				_ch[0]->mark_clear(_clear_val);
				_ch[1]->mark_clear(_clear_val);
				_clr = false;
			}
		}

		void update_size() {
			_size = 1 + _ch[0]->get_size() + _ch[1]->get_size();
		}

		void update_sum() {
			_sum = _val + _ch[0]->get_sum() + _ch[1]->get_sum();
		}

		void update_max_sum() {
			_max_sum = _ch[0]->get_max_rsum() + _val + _ch[1]->get_max_lsum();
			if (_ch[0]) _max_sum = max(_max_sum, _ch[0]->_max_sum);
			if (_ch[1]) _max_sum = max(_max_sum, _ch[1]->_max_sum);
		}

		void update_max_lsum() {
			_max_lsum = max(_ch[0]->get_max_lsum(), _ch[0]->get_sum() + _val + _ch[1]->get_max_lsum());
		}

		void update_max_rsum() {
			_max_rsum = max(_ch[1]->get_max_rsum(), _ch[1]->get_sum() + _val + _ch[0]->get_max_rsum());
		}

		void update() {					// 向上更新
			update_size();
			update_sum();
			update_max_sum();
			update_max_lsum();
			update_max_rsum();
		}
	};

	Node *_root;
	static Node *const _fa_root, _nodes[MAXMEM], *_st[MAXMEM];
	static int _mtot, _stop;

	void rotate(Node* x, int c) {    // 旋转操作，0 表示左旋，1 表示右旋
		Node* y = x->_fa;
		y->push_down(); x->push_down(); // y 在 x 之上，故先 y 后 x
		y->_ch[1 - c] = x->_ch[c];
		if (x->_ch[c])
			x->_ch[c]->_fa = y;
		x->_fa = y->_fa;
		if (y->_fa != _fa_root) {
			if (y->_fa->_ch[0] == y)
				y->_fa->_ch[0] = x;
			else
				y->_fa->_ch[1] = x;
		} else
			_root = x;
		x->_ch[c] = y;
		y->_fa = x;
		y->update();						// 维护 y
	}

	void splay(Node* x, Node *f) {    // 把结点 x 转到结点 f 下面
		x->push_down();
		while (x->_fa != f) {
			if (x->_fa->_fa == f) {
				if (x->_fa->_ch[0] == x)
					rotate(x, 1);
				else
					rotate(x, 0);
			} else {
				Node *y = x->_fa, *z = y->_fa;
				if (z->_ch[0] == y) {
					if (y->_ch[0] == x)
						rotate(y, 1), rotate(x, 1);
					else
						rotate(x, 0), rotate(x, 1);
				} else {
					if (y->_ch[1] == x)
						rotate(y, 0), rotate(x, 0);
					else
						rotate(x, 1), rotate(x, 0);
				}
			}
		}
		x->update();
	}

	Node* find_kth(int k) {
		Node* x = _root;
		x->push_down();				// notice!
		while (k != x->_ch[0]->get_size() + 1) {
			if (k <= x->_ch[0]->get_size()) {
				x = x->_ch[0];
			} else {
				k -= x->_ch[0]->get_size() + 1;
				x = x->_ch[1];
			}
			x->push_down();			// notice!
		}
		return x;
	}

	void build(int a, int b) {
		_root = make_tree(a, b);
		if (_root)
			_root->_fa = _fa_root;
	}

	static Node* make_tree(int a, int b) {
		if (a > b)
			return 0;
		int mid = (a + b) / 2;
		Node* root = new Node(arr[mid]);
		root->_ch[0] = make_tree(a, mid - 1);
		if (root->_ch[0])
			root->_ch[0]->_fa = root;
		root->_ch[1] = make_tree(mid + 1, b);
		if (root->_ch[1])
			root->_ch[1]->_fa = root;
		root->update();				// notice!
		return root;
	}

	void clear() {
		_root = 0;
	}

	static void mem_init() {
		_mtot = _stop = 0;
	}
};

template <class T>
typename Splay<T>::Node *const Splay<T>::_fa_root = 0;

template <class T>
typename Splay<T>::Node Splay<T>::_nodes[MAXMEM];

template <class T>
typename Splay<T>::Node* Splay<T>::_st[MAXMEM];

template <class T>
int Splay<T>::_stop = 0;

template <class T>
int Splay<T>::_mtot = 0;

int n, m;

Splay<int> tree;

char buf[100];

inline void pre_operation(int s, int e) {
	Splay<int>::Node *pa = tree.find_kth(s), *pb = tree.find_kth(e);
	tree.splay(pa, tree._fa_root);
	tree.splay(pb, tree._root);
}

inline void post_operation() {
	tree.splay(tree._root->_ch[1], tree._fa_root);
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
	int test;
	scanf("%d", &test);
	for (int cas = 1; cas <= test; ++cas) {
		tree.mem_init();
		scanf("%d%d", &n, &m);
		for (int i = 1; i <= n; ++i)
			scanf("%d", arr + i);
		tree.build(0, n + 1);
		for (int i = 0; i < m; ++i) {
			scanf("%s", buf);
			int k, t, v;
			switch (buf[0]) {
			case 'M':
				if (buf[2] == 'K') {	// MAKE-SAME
					scanf("%d%d%d", &k, &t, &v);
					pre_operation(k, k + t + 1);
					tree._root->_ch[1]->_ch[0]->mark_clear(v);
					post_operation();
				} else {				// MAX-SUM
					pre_operation(1, tree._root->get_size());
					printf("%d\n", tree._root->_ch[1]->_ch[0]->_max_sum);
				}
				break;
			case 'I': {					// INSERT
					scanf("%d%d", &k, &t);
					pre_operation(k + 1, k + 2);
					for (int i = 0; i < t; ++i)
						scanf("%d", arr + i);
					Splay<int>::Node* h = Splay<int>::make_tree(0, t - 1);
					tree._root->_ch[1]->_ch[0] = h;
					if (h) h->_fa = tree._root->_ch[1];
					post_operation();
				}
				break;
			case 'D': {					// DELETE
					scanf("%d%d", &k, &t);
					pre_operation(k, k + t + 1);
					Splay<int>::Node* h = tree._root->_ch[1]->_ch[0];
					tree._root->_ch[1]->_ch[0] = 0;
					if (h) h->recycle();
					post_operation();
				}
				break;
			case 'R': {					// REVERSE
					scanf("%d%d", &k, &t);
					pre_operation(k, k + t + 1);
					tree._root->_ch[1]->_ch[0]->mark_rev();
					post_operation();
				}
				break;
			case 'G': {					// GET-SUM
					scanf("%d%d", &k, &t);
					pre_operation(k, k + t + 1);
					printf("%d\n", tree._root->_ch[1]->_ch[0]->get_sum());
				}
				break;
			}
		}
	}
	return 0;
}

比较麻烦的题，两种标记，_clr 和 _rev 都有，然后还有插入删除，以及最最ws的 MAX-SUM 询问，最后加起来，结点内信息的个数就相当恐怖了。再加上是在十分疲劳的状态下写的，于是 RE 和 WA了 N 次之后，终于 AC 。首先，这题的数据里，有一个 GET-SUM 的 tot 是 0 ，会导致非法解引用，找出这个错误，花了大概 N/3 个 RE 。之后一直 WA ，最后发现，原来是 mark_clear 里面，_val 忘记更新了，囧~ 这个错误真是太水了。这题最麻烦的还是两个标记的处理，我的做法是延续线段树时代的做法，由于 _clr 的特殊性质，每次保证标记信息中 _clr 和 _rev 里面只有一个为 true ，然后就好处理了。还有就是在 DELETE 那个地方，我纠结了好久，终于决定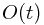的方式返还内存了。开始是想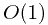返还内存的，但是想到普通实现用 new 的时候就会  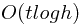，觉得得不偿失，最后没有采用。忽然想到一种 del 操作 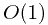new 操作 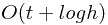的实现，不过比较麻烦，那就以后实现吧。

最后有个小插曲，我发现，在 SPOJ 上 AC 的代码，在衡阳八中 OJ 上，居然 WA 了。一开始以为是数据错了，搞了半天发现，果然是数据问题，SPOJ 把数据合并了，开头有个 test ，而衡阳八中 OJ 是原始 NOI2005 数据，开头没有 test 。做到这里，我差点晕过去，果然状态不好的时候不应该碰这种繁琐题的 =           =...

ps. 今天还有个插曲，我居然想不通如何维护乘法和加法的标记延迟了，囧~ 这什么状态，最后经大神提醒，终于知道怎么搞了。唉，看来今天是比较悲剧的。。。

其实这题很早就想 AC 了。题目描述超短，做题思路也是比较清晰的：以 sa 的下标为结点和关键字，以区间内的 height 数组为优先级构造笛卡尔树，然后进行检索即可。我比较懒，直接就用 RMQ 来计算左右子树的分界点了，想 O(n) 构造笛卡尔树的话，可以用一个栈维护右链的方法得到。如果对这种构造方法不是很熟练的话，可以拿理工邀请赛的 F 题 (hdu 3410) 练下手。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define MAXN 100000
#define MAXM 128			// 字母个数

int head[MAXN], succ[MAXN], succRank[MAXN];
int sa[MAXN], rank[MAXN];
int letter[MAXM];

void da(char* str, int len) {	// 倍增算法
	memset(letter, 0, sizeof(letter));
	for (int i = 0; i < len; ++i)
		if (!letter[str[i]])
			letter[str[i]] = 1;
	int total = -1;
	for (int i = 0; i < MAXM; ++i)
		if (letter[i])
			letter[i] = ++total;
	memset(head, 255, sizeof(head));
	for (int i = len - 1; i >= 0; --i) {	// 由于 head 头指针的性质，所以要倒序添加，下同
		rank[i] = letter[str[i]];
		succ[i] = head[rank[i]];
		head[rank[i]] = i;
	}
	int j = 0;
	for (int i = 0; i < len; ++i) {
		while (head[j] == -1) ++j;
		sa[i] = head[j];
		head[j] = succ[head[j]];
	}
	// 到此初始化排序完毕
	for (int k = 1; k < len; k <<= 1) {
		// 以下两个 for 对新一轮子串进行排序，由于第二关键字的排序在上一次排序中已完成
		// 故仅对第一关键字进行排序即可
		for (int i = len - 1; i >= 0; --i)		// 倒序添加
			if (sa[i] - k >= 0) {
				succRank[sa[i] - k] = rank[sa[i]];
				succ[sa[i] - k] = head[rank[sa[i] - k]];
				head[rank[sa[i] - k]] = sa[i] - k;
			}
		for (int i = len - 1; i >= len - k; --i) {	// 倒序添加
			succRank[i] = -1;					// 另外添加的尾字符的 rank 为 -1
			succ[i] = head[rank[i]];
			head[rank[i]] = i;
		}
		j = 0; total = -1;
		int preSuccRank = 0, preRank = 0;
		for (int i = 0; i < len; ++i) {
			while (head[j] == -1) ++j;
			sa[i] = head[j];
			if (i == 0 || preRank != rank[sa[i]] || preSuccRank != succRank[sa[i]]) {
				preRank = rank[sa[i]];
				rank[sa[i]] = ++total;	// 链表中保证不递减，所以可以这么做
			} else {
				preRank = rank[sa[i]];
				rank[sa[i]] = total;
			}
			preSuccRank = succRank[sa[i]];
			head[j] = succ[head[j]];
		}
	}
}

int height[MAXN];
long long mem[MAXN + 1], *sumLength = mem + 1;

void calcHeight(char* str, int len) {
	int i, j, k = 0;
	for (i = 0; i < len; ++i) {
		if (k != 0)				// h[i] >= h[i - 1] - 1
			--k;
		if (rank[i] == 0)
			continue;
		j = sa[rank[i] - 1];
		// 求 suffix(sa[rank[i] - 1]) 和 suffix(sa[rank[i]]) 的最大公共前缀
		while (str[i + k] == str[j + k])		// C 字符串以 '\0' 结尾
			++k;
		height[rank[i]] = k;	// h[i] = k;
	}
}

int minData[MAXN + 1][18];

inline int minHeight(int x, int y) {
	return height[x] <= height[y] ? x : y;
}

inline void initRMQ(int s, int e) {
	if (s > e)
		return;
	for (int i = s; i <= e; ++i)
		minData[i][0] = i;
	int h = (int)(log(e - s + 1.0) / log(2.0));
	for (int j = 1; j <= h; ++j)
		for (int i = s; i + (1 << j) - 1 <= e; ++i)
			minData[i][j] = minHeight(minData[i][j - 1], minData[i + (1 << (j - 1))][j - 1]);
}

inline int askRMQ(int a, int b) {
	int l = (int)(log(b - a + 1.0) / log(2.0));
	return minHeight(minData[a][l], minData[b - (1 << l) + 1][l]);
}

inline int lcp(int a, int b) {
	return height[askRMQ(std::min(rank[a], rank[b]) + 1, std::max(rank[a], rank[b]))];
}

char buf[MAXN + 2];
long long k;

int rk, rl;

void getAnswer(long long a, long long b) {
	int h = 0;
	while (a != b) {
		int idx = askRMQ(a + 1, b) - 1;
		if (k <= (height[idx + 1] - h) * (b - a + 1)) {
			rk = a; rl = h + 1 + (k - 1) / (b - a + 1);
			return;
		}
		k -= (height[idx + 1] - h) * (b - a + 1);
		if (k <= sumLength[idx] - sumLength[a - 1] - height[idx + 1] * (idx - a + 1)) {
			b = idx; h = height[idx + 1];
			continue;
		}
		k -= sumLength[idx] - sumLength[a - 1] - height[idx + 1] * (idx - a + 1);
		a = idx + 1;
		h = height[idx + 1];
	}
	rk = a; rl = h + k;
}

int main() {
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int test;
	scanf("%d", &test);
	for (int cas = 1; cas <= test; ++cas) {
		scanf("%s%I64d", buf, &k);
		int len = strlen(buf);
		da(buf, len);
		calcHeight(buf, len);

		for (int i = 0; i < len; ++i)
			sumLength[i] = sumLength[i - 1] + len - sa[i];
		initRMQ(1, len - 1);
		getAnswer(0, len - 1);

		printf("Case %d: ", cas);
		for (int i = 0; i < rl; ++i)
			putchar(buf[sa[rk] + i]);
		putchar('\n');
	}
	return 0;
}

经典的树套树，顺便测一下自己的模板。奇怪的是使用通用模板反而比特别优化的直接寻址要快。

这个是最终版本：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define MAXN 50005

template <class T>
struct Splay {
	struct Node {
		Node *_fa, *_ch[2];
		T _val;
		int _size;

		Node() {}
		Node(const T& x) { set_value(x); }

		void *operator new(size_t) {
			if (_stop != 0) return _st[--_stop];
			else return _nodes + _mtot++;
		}

		void operator delete(void* p, size_t) {
			_st[_stop++] = (Node*)p;
		}

		void set_value(const T& x) {
			_val = x; _size = 1;
			_ch[0] = _ch[1] = 0;
			_fa = _fa_root;
		}

		Node* get_end(int c) {            // 0 表示左端 1 表示右端
			Node* x = this;
			while (x->_ch[c])
				x = x->_ch[c];
			return x;
		}

		Node* get_near(int c) {
			if (_ch[c])
				return _ch[c]->get_end(1 - c);
			Node* x = this;
			while (x->_fa && x->_fa->_ch[c] == x)
				x = x->_fa;
			return x->_fa;
		}

		Node* get_succ() { return get_near(1); }
		Node* get_prev() { return get_near(0); }

		void push_down() {}				// 向下传标记
		void update() {
			_size = 1;
			if (_ch[0]) _size += _ch[0]->_size;
			if (_ch[1]) _size += _ch[1]->_size;
		}

		int get_size() {
			if (this) return _size;
			else return 0;
		}
	};

	Node *_root;
	static Node *const _fa_root, _nodes[(MAXN + 1) * 18], *_st[(MAXN + 1) * 18];
	static int _mtot, _stop;

	void rotate(Node* x, int c) {    // 旋转操作，0 表示左旋，1 表示右旋
		Node* y = x->_fa;
		y->push_down(); x->push_down(); // y 在 x 之上，故先 y 后 x
		y->_ch[1 - c] = x->_ch[c];
		if (x->_ch[c])
			x->_ch[c]->_fa = y;
		x->_fa = y->_fa;
		if (y->_fa != _fa_root) {
			if (y->_fa->_ch[0] == y)
				y->_fa->_ch[0] = x;
			else
				y->_fa->_ch[1] = x;
		} else
			_root = x;
		x->_ch[c] = y;
		y->_fa = x;
		y->update();						// 维护 y
	}

	void splay(Node* x, Node *f) {    // 把结点 x 转到结点 f 下面
		x->push_down();
		while (x->_fa != f) {
			if (x->_fa->_fa == f) {
				if (x->_fa->_ch[0] == x)
					rotate(x, 1);
				else
					rotate(x, 0);
			} else {
				Node *y = x->_fa, *z = y->_fa;
				if (z->_ch[0] == y) {
					if (y->_ch[0] == x)
						rotate(y, 1), rotate(x, 1);
					else
						rotate(x, 0), rotate(x, 1);
				} else {
					if (y->_ch[1] == x)
						rotate(y, 0), rotate(x, 0);
					else
						rotate(x, 1), rotate(x, 0);
				}
			}
		}
		x->update();
	}

	Node* join(Node* r1, Node* r2) {
		if (r1 && r2) {
			Node *right_end = r1->get_end(1);
			splay(right_end, r1->_fa);
			right_end->_ch[1] = r2;
			r2->_fa = right_end;
			right_end->update();
			return right_end;
		}
		if (r1) return r1;
		if (r2) return r2;
		return 0;
	}

	void insert(const T& px) {
		Node* nd = new Node(px);
		if (_root == 0) {
			_root = nd;
			return;
		}
		Node *x = _root, *y = _fa_root;
		while (x) {
			y = x;
			if (nd->_val <= x->_val)
				x = x->_ch[0];
			else
				x = x->_ch[1];
		}
		if (nd->_val <= y->_val)
			y->_ch[0] = nd;
		else
			y->_ch[1] = nd;
		nd->_fa = y;
		splay(nd, _fa_root);
	}

	void erase(const T& px) {
		Node* nd = lower_bound(px);
		if (nd == 0 || nd->_val != px)
			return;
		Node* x = join(nd->_ch[0], nd->_ch[1]);
		if (nd->_fa == _fa_root) {
			_root = x;
		} else {
			if (nd->_fa->_ch[0] == nd)
				nd->_fa->_ch[0] = x;
			else
				nd->_fa->_ch[1] = x;
		}
		if (x)
			x->_fa = nd->_fa;
		if (nd->_fa)
			splay(nd->_fa, _fa_root);
		delete nd;
	}

	Node* lower_bound(const T& px) {
		Node *x = _root, *y = _fa_root;
		while (x) {
			y = x;
			if (px <= x->_val)
				x = x->_ch[0];
			else
				x = x->_ch[1];
		}
		if (y == _fa_root)
			return 0;
		if (px <= y->_val)
			return y;
		else
			return y->get_succ();
	}

	Node* upper_bound(const T& px) {
		Node *x = _root, *y = _fa_root;
		while (x) {
			y = x;
			if (px < x->_val)
				x = x->_ch[0];
			else
				x = x->_ch[1];
		}
		if (y == _fa_root)
			return 0;
		if (px < y->_val)
			return y;
		else
			return y->get_succ();
	}

	int query_less(const T& val) {
		Node* x = lower_bound(val);
		if (x == 0)
			return _root->get_size();
		splay(x, _fa_root);
		return x->_ch[0]->get_size();
	}

	void clear() {
		_root = 0;
	}

	static void mem_init() {
		_mtot = _stop = 0;
	}
};

template <class T>
typename Splay<T>::Node *const Splay<T>::_fa_root = 0;

template <class T>
typename Splay<T>::Node Splay<T>::_nodes[(MAXN + 1) * 18];

template <class T>
typename Splay<T>::Node* Splay<T>::_st[(MAXN + 1) * 18];

template <class T>
int Splay<T>::_stop = 0;

template <class T>
int Splay<T>::_mtot = 0;

int v[MAXN + 1];

struct Node {
	int _a, _b;
	Node *_left, *_right;
	Splay<int> _bst;
} nodes[MAXN * 2], *ptr;

void build_tree(int a, int b) {
	Node* root = ++ptr;
	root->_a = a; root->_b = b;
	root->_bst.clear();
	root->_bst.insert(v[a]);
	if (a == b) {
		root->_left = root->_right = 0;
		return;
	}
	for (int i = a + 1; i <= b; ++i)
		root->_bst.insert(v[i]);
	root->_left = ptr + 1;
	build_tree(a, (a + b) / 2);
	root->_right = ptr + 1;
	build_tree((a + b) / 2 + 1, b);
}

int la, lb, lk;

void modify(Node* root) {
	if (root->_a == root->_b) {
		root->_bst.erase(v[la]);
		root->_bst.insert(v[la] = lk);
		return;
	}
	root->_bst.erase(v[la]);
	root->_bst.insert(lk);
	int mid = (root->_a + root->_b) / 2;
	if (la <= mid)
		modify(root->_left);
	else
		modify(root->_right);
}

int query(Node* root) {
	if (la <= root->_a && root->_b <= lb) {
		return root->_bst.query_less(lk);
	}
	int mid = (root->_a + root->_b) / 2;
	int res = 0;
	if (la <= mid)
		res = query(root->_left);
	if (mid < lb)
		res += query(root->_right);
	return res;
}

inline int solve(int a, int b, int k) {
	int l = 0, r = 1000000001, mid;
	while (l + 1 != r) {
		mid = (l + r) / 2;
		la = a; lb = b; lk = mid;
		if (query(nodes + 1) < k)
			l = mid;
		else
			r = mid;
	}
	return l;
}

int main() {
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int test;
	scanf("%d", &test);
	for (int cas = 1; cas <= test; ++cas) {
		Splay<int>::mem_init();
		int n, m;
		scanf("%d%d", &n, &m);
		for (int i = 1; i <= n; ++i)
			scanf("%d", v + i);
		ptr = nodes;
		build_tree(1, n);
		for (int i = 1; i <= m; ++i) {
			char c;
			int a, b, k;
			scanf(" %c", &c);
			if (c == 'Q') {
				scanf("%d%d%d", &a, &b, &k);
				printf("%d\n", solve(a, b, k));
			} else {
				scanf("%d%d", &a, &k);
				la = a; lk = k;
				modify(nodes + 1);
			}
		}
	}
	return 0;
}

第二个版本，就是 query 的时候不进行 splay 操作，比上面的程序略慢一些：

int query_less(const T& val) {
		int res = 0;
		Node* x = _root;
		while (x) {
			if (val <= x->_val) {
				x = x->_ch[0];
			} else {
				++res;
				if (x->_ch[0])
					res += x->_ch[0]->_size;
				x = x->_ch[1];
			}
		}
		return res;
	}

原始版本，8s 水过 =          =... 让我不得不怀疑是不是 gcc 的寻址有些问题。

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define MAXN 50005

struct Splay {
	struct Node {
		Node *_fa, *_ch[2];
		int _val, _size;
		void update() {
			_size = 1;
			if (_ch[0]) _size += _ch[0]->_size;
			if (_ch[1]) _size += _ch[1]->_size;
		}
		void set_value(int x) {
			_size = 1; _val = x;
			_ch[0] = _ch[1] = 0; _fa = _fa_root;
		}
		Node* get_end(int c) {			// 0 表示左端 1 表示右端
			Node* x = this;
			while (x->_ch[c])
				x = x->_ch[c];
			return x;
		}
	};

	Node *_root;
	static Node *const _fa_root, _nodes[MAXN + 1][18];

	void rotate(Node* x, int c) {	// 旋转操作，0 表示左旋，1 表示右旋
		Node* y = x->_fa;
		y->_ch[1 - c] = x->_ch[c];
		if (x->_ch[c])
			x->_ch[c]->_fa = y;
		x->_fa = y->_fa;
		if (y->_fa != _fa_root) {
			if (y->_fa->_ch[0] == y)
				y->_fa->_ch[0] = x;
			else
				y->_fa->_ch[1] = x;
		} else
			_root = x;
		x->_ch[c] = y;
		y->_fa = x;
		y->update();
	}

	void splay(Node* x, Node *f) {	// 把结点 x 转到结点 f 下面
		while (x->_fa != f) {
			if (x->_fa->_fa == f) {
				if (x->_fa->_ch[0] == x)
					rotate(x, 1);
				else
					rotate(x, 0);
			} else {
				Node *y = x->_fa, *z = y->_fa;
				if (z->_ch[0] == y) {
					if (y->_ch[0] == x)
						rotate(y, 1), rotate(x, 1);
					else
						rotate(x, 0), rotate(x, 1);
				} else {
					if (y->_ch[1] == x)
						rotate(y, 0), rotate(x, 0);
					else
						rotate(x, 1), rotate(x, 0);
				}
			}
		}
		x->update();
	}

	Node* join(Node* r1, Node* r2) {
		if (r1 && r2) {
			Node *right_end = r1->get_end(1);
			splay(right_end, r1->_fa);
			right_end->_ch[1] = r2;
			r2->_fa = right_end;
			right_end->update();
			return right_end;
		}
		if (r1) return r1;
		if (r2) return r2;
		return 0;
	}

	void insert(Node* nd) {
		Node *x = _root, *y = _fa_root;
		while (x) {
			y = x;
			if (nd->_val < x->_val)
				x = x->_ch[0];
			else
				x = x->_ch[1];
		}
		if (nd->_val < y->_val)
			y->_ch[0] = nd;
		else
			y->_ch[1] = nd;
		nd->_fa = y;
		splay(nd, _fa_root);
	}

	void erase(Node* nd) {
		Node* x = join(nd->_ch[0], nd->_ch[1]);
		if (nd->_fa == _fa_root) {
			_root = x;
		} else {
			if (nd->_fa->_ch[0] == nd)
				nd->_fa->_ch[0] = x;
			else
				nd->_fa->_ch[1] = x;
		}
		if (x)
			x->_fa = nd->_fa;
		if (nd->_fa)    // 需要更新的是父结点以及父的所有父，x 结点在 join 时已更新
			splay(nd->_fa, _fa_root);
	}

	int query_less(int val) {
		int res = 0;
		Node* x = _root;
		while (x) {
			if (val <= x->_val) {
				x = x->_ch[0];
			} else {
				++res;
				if (x->_ch[0])
					res += x->_ch[0]->_size;
				x = x->_ch[1];
			}
		}
		return res;
	}
};

Splay::Node *const Splay::_fa_root = 0, Splay::_nodes[MAXN + 1][18];

int v[MAXN + 1];

struct Node {
	int _a, _b, _dep;
	Node *_left, *_right;
	Splay _bst;
} nodes[MAXN * 2], *ptr;

void build_tree(int a, int b, int dep) {
	Node* root = ++ptr;
	root->_a = a; root->_b = b;
	root->_dep = dep;
	root->_bst._root = Splay::_nodes[a] + dep;
	root->_bst._root->set_value(v[a]);
	if (a == b) {
		root->_left = root->_right = 0;
		return;
	}
	for (int i = a + 1; i <= b; ++i) {
		Splay::_nodes[i][dep].set_value(v[i]);
		root->_bst.insert(Splay::_nodes[i] + dep);
	}
	root->_left = ptr + 1;
	build_tree(a, (a + b) / 2, dep + 1);
	root->_right = ptr + 1;
	build_tree((a + b) / 2 + 1, b, dep + 1);
}

int la, lb, lk;

void modify(Node* root) {
	if (root->_a == root->_b) {
		root->_bst._root->set_value(v[root->_a] = lk);
		return;
	}
	root->_bst.erase(Splay::_nodes[la] + root->_dep);
	Splay::_nodes[la][root->_dep].set_value(lk);
	root->_bst.insert(Splay::_nodes[la] + root->_dep);
	int mid = (root->_a + root->_b) / 2;
	if (la <= mid)
		modify(root->_left);
	else
		modify(root->_right);
}

int query(Node* root) {
	if (la <= root->_a && root->_b <= lb) {
		return root->_bst.query_less(lk);
	}
	int mid = (root->_a + root->_b) / 2;
	int res = 0;
	if (la <= mid)
		res = query(root->_left);
	if (mid < lb)
		res += query(root->_right);
	return res;
}

inline int solve(int a, int b, int k) {
	int l = 0, r = 1000000001, mid;
	while (l + 1 != r) {
		mid = (l + r) / 2;
		la = a; lb = b; lk = mid;
		if (query(nodes + 1) < k)
			l = mid;
		else
			r = mid;
	}
	return l;
}

int main() {
#ifndef ONLINE_JUDGE
	freopen("in.txt", "r", stdin);
	freopen("out.txt", "w", stdout);
#endif
	int test;
	scanf("%d", &test);
	for (int cas = 1; cas <= test; ++cas) {
		int n, m;
		scanf("%d%d", &n, &m);
		for (int i = 1; i <= n; ++i)
			scanf("%d", v + i);
		ptr = nodes;
		build_tree(1, n, 0);
		for (int i = 1; i <= m; ++i) {
			char c;
			int a, b, k;
			scanf(" %c", &c);
			if (c == 'Q') {
				scanf("%d%d%d", &a, &b, &k);
				printf("%d\n", solve(a, b, k));
			} else {
				scanf("%d%d", &a, &k);
				la = a; lk = k;
				modify(nodes + 1);
			}
		}
	}
	return 0;
}